Box Muller Transform

The Box–Muller transform is a method for generating pairs of independent, standard, normally distributed random numbers, given a source of uniformly distributed random numbers.

The Box–Muller transform is commonly expressed in two forms. The basic form takes two samples from the uniform distribution on the interval [0, 1] and maps them to two standard, normally distributed samples. The polar form takes two samples from a different interval, [−1, +1], and maps them to two normally distributed samples without the use of sine or cosine functions. Basic form:

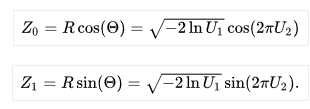
Let’s say U1 and U2 are our original independent random variables; they are uniformly distributed in the interval (0,1). The Box-Muller transformation creates new Z0 and Z1; independent, random variables that have a standard normal distribution. Polar form:

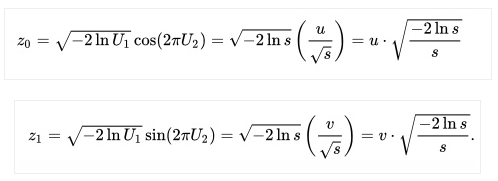
The polar method can be faster than the basic method because it is simpler to compute and is more numerically robust. It avoids the use of trigonometric functions, which can be expensive in some computing environments.

The basic form requires two multiplications, logarithm, square root, and one trigonometric function for each normal variate.

So a Box Muller transform takes a continuous, two dimensional uniform distribution and transforms it to a normal distribution. It is widely used in statistical sampling, and is an easy to run, elegant way to come up with a standard normal model.

At its most basic, the Box-Muller transformations simply takes two variables that are uniformly distributed and sends them to two independent random variables with a standard normal distribution.