Markov’s inequality is a helpful result in probability that gives information about a probability distribution. The remarkable aspect about it is that the inequality holds for any distribution with positive values, no matter what other features that it has. Markov’s inequality gives an upper bound for the percent of the distribution that is above a particular value.
Markov’s inequality says that for a positive random variable X and any positive real number a, the probability that X is greater than or equal to a is less than or equal to the expected value of X divided by a.
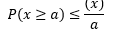
The above description can be stated more succinctly using mathematical notation. In symbols we write Markov’s inequality as:
For example we suppose a student is extracted at random from a group of students having an weight of 80 kg. What is the probability that the extracted student’s weight is greater than 20 kg? In the absence of more information about the distribution of weight, we can use Markov’s inequality to calculate an upper bound to this probability. Therefore, the probability of extracting a student having an weight greater than 20 kg is less than 1/4.
Statistics Lessons Blog 