The Weak Law of Large Numbers, also known as Bernoulli’s theorem, states that if you have a sample ofindependent and identically distributed random variables, as the sample size grows larger, the sample mean will tend toward the population mean.
More formally, the central limit theorem can be defined as follows: for the sample size→∞ the arithmetic average tends more and more closely to the expected value E(X)=μ. In other words, given a set of random variables with expected value μ and variance σ2, for every d > 0:
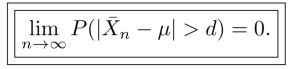
We can prove this using Chebyshev’s inequality, which says the probability that a random variable X differs from its mean by some small constant d is less than or equal to the variance of X divided by the the square of the constant d.
In few words, the theorem states that the sum of N independent variables (that is, the mean) tends for an always greater number N of variables to the normal distribution regardless of the effective distribution of each single variable (but equal for all). As n tends to infinity, it follows that the right side of the inequality equals 0.
Statistics Lessons Blog 